Construções geométricas rigorosas
Multiplicação geométrica
Construir um segmento de reta, cuja medida seja o produto de dois comprimentos dados.
Use os botões de controlo para mostrar os passos da construção. Pode arrastar os pontos e verificar as alterações e as relações que se matêm invariantes.
Veja uma demonstração que justifica o facto do segmento construído medir o produto dos segmentos dados, recorrendo à semelhança de triângulos.
|
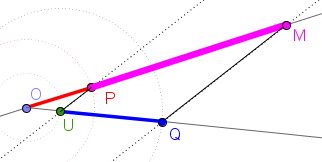
Como $ \bigtriangleup [OPU] \equiv \; \bigtriangleup [OMQ] $, temos que: $\frac{\overline{OP}+\overline{PM}}{\overline{OP}} = \frac{\overline{OU}+\overline{UQ}}{\overline{OU}} $ ou seja, $\frac{\overline{OP}}{\overline{OP}} + \frac{\overline{PM}}{\overline{OP}}= \frac{\overline{OU}}{\overline{OU}}+\frac{\overline{UQ}}{\overline{OU}} \Leftrightarrow 1 + \frac{\overline{PM}}{\overline{OP}}= 1 +\frac{\overline{UQ}}{\overline{OU}} \Leftrightarrow $ $\Leftrightarrow \frac{\overline{PM}}{\overline{OP}}= \frac{\overline{UQ}}{\overline{OU}}$ e como $\small{ \overline{OU} =1} $ $ \frac{\overline{PM}}{\overline{OP}}= \frac{\overline{UQ}}{1} \Leftrightarrow \frac{\overline{PM}}{\overline{OP}}= \small{\overline{UQ}} \Leftrightarrow \small{\overline{PM}=\overline{OP} \times \overline{UQ}}$ |
A animação apresentada foi construída com o programa GeoGebra.
